Blog

Jaja, der Winter. Die Tage werden kürzer, die Wochen länger … oder so.

Zuerst einmal die Auflösung: die Wahrscheinlichkeit, dass sich jemand beim Wichteln selbst zieht, liegt bei stolzen 63,2 %. Etwa 2 von 3 Versuchen gehen also schief.

Fragen wir uns zunächst einmal wie viele Möglichkeiten es überhaupt gibt, n Zettel mit Namen an n Personen zu verteilen. Die erste Person, die in den Beutel greift, hat noch alle n Zettel zur Auswahl, die nachfolgende nur noch n - 1 und die nächste n - 2. Die vorletzte hat noch die Auswahl zwischen 2 Zetteln und die letzte muss den letzten Zettel aus dem Beutel greifen. Ergibt also: n ⋅ (n - 1) ⋅ … ⋅ 2 ⋅ 1. Diese Funktion nennt man in der Mathematik die Fakultät einer Zahl und wird n! abgekürzt. Das kombinatorische Prinzip dahinter heißt übrigens Permutation und beschreibt, wie eine Menge von n Elementen auf die selbe Menge mit n Elementen abgebildet werden kann.

Nun gibt es besondere Permutationen, bei denen sichergestellt ist, dass kein Element auf sich selbst abgebildet wird. Diese nennt man fixpunktfreie Permutationen und ich musste selbst erst einmal nachschlagen, wie man deren Anzahl bei n Elementen berechnet: mit der Subfakultät, die !n abgekürzt wird. Und so sieht die Formel dazu aus:

Nun haben wir alles beisammen, was wir brauchen. Um zu bestimmen, wie hoch die Wahrscheinlichkeit ist, dass jemand beim Wichteln sich selbst zieht, berechnen wir die Gegenwahrscheinlichkeit aus dem Verhältnis zwischen der Anzahl der fixpunktfreien Permutationen (niemand zieht sich selbst) und der Anzahl der Permutationen überhaupt:

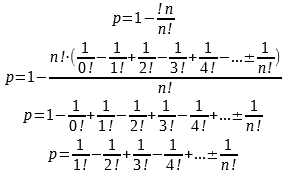
Nach der letzten Kürzung sieht das doch schon ganz brauchbar aus. Tabellieren wir das mal in Abhängigkeit von n und man sieht, dass sich die Wahrscheinlichkeit ab 5 Personen kaum noch ändert:

Fun Fact zum Schluss: Der Grenzwert ist übrigens … (Trommelwirbel) …

[unterstützt durch Produktplatzierungen]

Es kommt wieder die Zeit, in der in vielen Betrieben, Freundeskreisen und in der Schule gewichtelt wird. In der Regel gibt man dazu die Namen aller Teilnehmer auf Zetteln in einen Beutel und lässt nacheinander daraus ziehen. Ärgerlicherweise kann es dabei natürlich passieren, dass jemand in der Runde sich selbst zieht und man wieder von vorne beginnen kann. Da drängt sich natürlich jedem¹ sofort die Frage auf: wie wahrscheinlich ist es eigentlich, dass mindestens eine Person sich selbst zieht?

Ausschnitt eines nachbearbeiteten Bildes von: whatleydude@flickr – Lizenz: CC-by

Für einen kleinen Teilnehmerkreis (ich nenne die Anzahl der Personen im Folgenden n) ist die Sache leicht zu berechnen. Für n = 1 ist die Chance, dass diese eine Person sich selbst zieht, bei 100 %. Außerdem ist es sehr traurig.

Für n = 2 geht die Sache entweder perfekt aus, weil jeder den anderen zieht, oder jeder zieht sich selbst; macht 50 % und ist das Gegenteil von spannend.

Erst für n = 3 wird die Sache langsam spannender und erstaunlicherweise nähert sich die Wahrscheinlichkeit, dass jemand in der Runde sich selbst zieht, sehr schnell einem Grenzwert an, sodass die Anzahl der Teilnehmer keine wesentliche Rolle spielt. Man kann also die Frage von oben ziemlich pauschal mit einem konkreten Prozentwert beantworten.

Die Antwort darauf gibt es in etwa einer Woche. Wer will, kann gerne in die Kommentare seine Vermutung posten.

_____
¹: normale Menschen ausgeschlossen